폴리시 그레이디언트

정책 기반 강화학습

  • 그간 배웠던 강화학습은 가치 기반이다. 가치 기반은 가치함수를 기반으로 행동을 선택하고 업데이트하면서 학습한다.
  • 정책 기반 강화학습은 가치함수를 토대로 행동을 결정하지 않고 상태에 따로 바로 행동을 선택한다.
  • 큐함수를 근사했던 딥살사와 달리 정책 기반에서는 인공신경망이 정책을 근사한다.
  • 정책신경망(정책을 근사하는 인공신경망)에서는 출력층의 활성함수가 Softmax함수이다.

Softmax함수란?

  • Softmax함수는 출력이 다 합해서 1이 나오기 원할 때 사용한다.
  • 이를 사용하는 이유는 바로 정책의 정의가 바로 각 행동을 할 확률이기 때문이다.
  • 그렇다면 정책 기반 강화학습의 목표는 무엇일까?

폴리시 그레이디언트

  • 정책신경망을 사용할 경우에 정책신경망의 계수에 따라 누적보상이 달라질 것이다.
  • 때문에 정책기반 강화학습의 목표 또한 좋은 정책 신경망의 계수를 찾는 것이다.
  • 기존 정책은 상태마다 행동에 따라 확률이 주어지지만 이제는 정책신경망이 정책을 대체하게 된다.
  • 아래와 같이 정책 신경망의 가중치값(쎄타)으로 정책을 표현할 수 있다.

사진

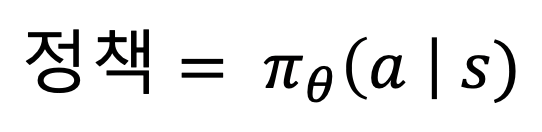
  • 이 때 위에 나오는 쎄타를 최적화하는 것이 목표이다. 정책을 최적화하는 목표함수(Objective Fuction)를 J라고 하자.
  • 목표함수 J를 최적화하는 방법은 목표함수를 미분해서 그 미분값에 따라 정책을 업데이트하는 것이다.
  • 오류함수를 최소화하는 것과 달리 여기서는 목표함수를 최대화 해야한다.
  • 따라서 경사상승법(Gradient Ascent)이라고 부른다.
  • 경사상승법에 따라 정책 신경망을 업데이트하는 것을 수식으로 나타내면 다음과 같다.

사진

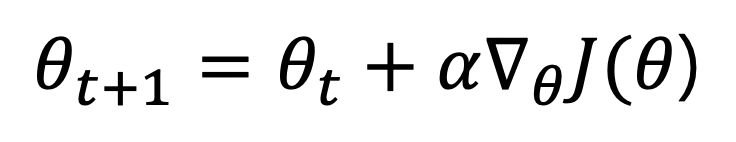
  • 위의 식에서 역삼각형 밑에 쎄타가 있는 기호는 쎄타에 대해 미분을 하는 기호다.
  • 시점이 지날 때마다 현재 값에 미분값의 일정치를 더해줌으로써 정책 신경망을 업데이트한다.
  • 이를 Policy Gradient(폴리시 그레이디언트)라고 한다.

목표함수는 어떻게 정의될 수 있나?

  • 그것은 주로 2가지 방법에 의해서 정의될 수 있다.
  • 1.게임과 같은 경우에는 첫 state의 가치함수가 최대로 만들 대상이 된다.(이 때는 가치함수를 미분해야함으로 쉽지않다.)
  • 2.각 time step마다 받을 수 있는 reward의 평균값이 최대로 만들 대상이 된다.
  • 두번쨰 방법은 리처트 서튼의 Policy Gradient Methods for Reinforcement Learing with Function Approximation”에서 소개되었다.
  • 거기서 소개된 폴리시 그레이디언트 정리(Policy Gradient Theorem)은 다음과 같다.

사진

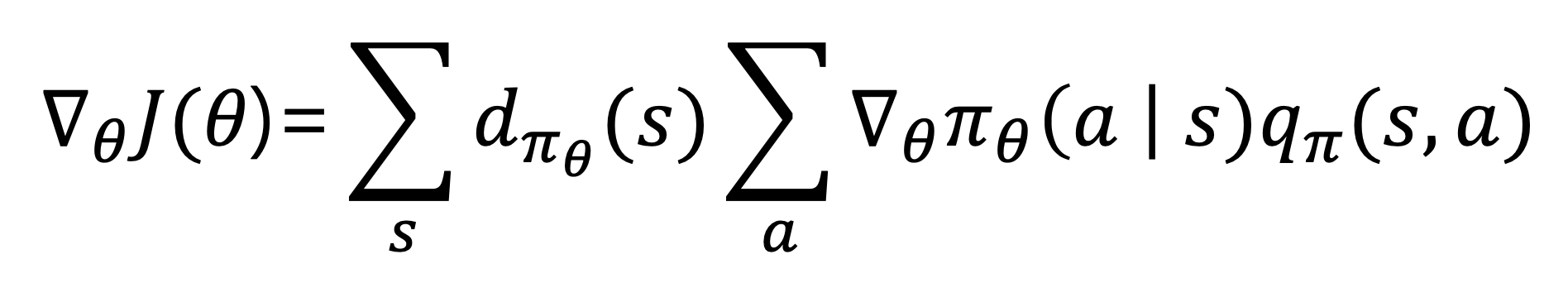
  • 위 식에서 첫 summation은 에이전트가 s라는 상태에 있을 확률을 의미한다.
  • 위의 수식은 가능한 모든 상태에 대해 각 상태에서 특정행동을 했을 때 받을 수 있는 큐함수의 기댓값을 의미한다.
  • 위 수식은 log 함수의 미분에 따라 다음과 같이 표현할 수도 있다.

사진

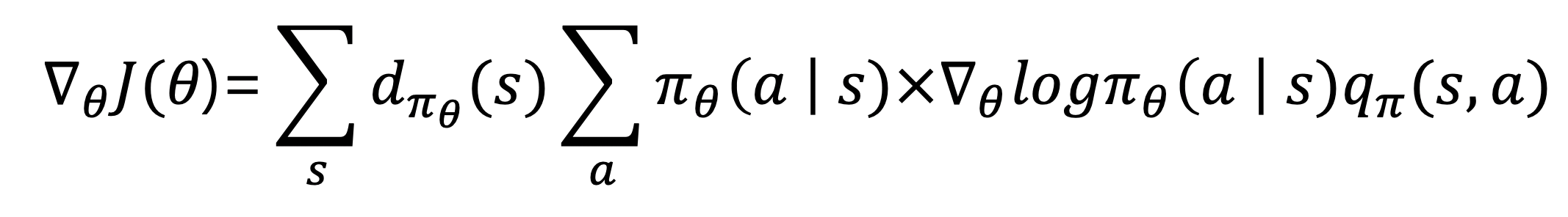
  • 우변 중에서 곱셈 좌측은 에이전트가 어떤 상태 s에서 행동 a를 선택할 확률을 의미한다.
  • 기댓값의 정의가 확률 x 받은 값 이라고 한다면, 이는 기댓값으로 표현 가능한다.
  • 즉, 최종적으로 얻은 목표함수의 미분값에 대한 수식은 다음과 같다.

사진

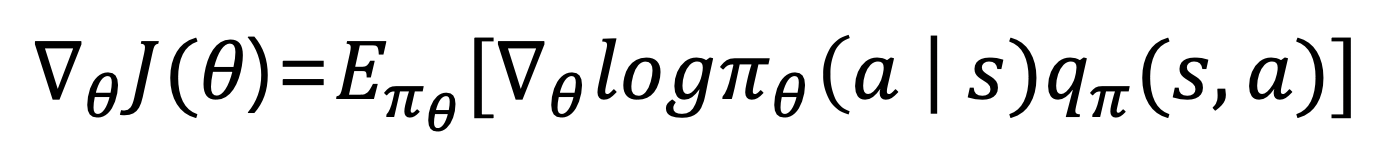
  • 결국 에이전트가 정책신경망을 업데이트하기 위해 구해야하는 식은 기댓값 괄호 안에 있는 값이다.
  • 결국 폴리시 그레이언트 업데이트 식은 다음과 같다.

사진

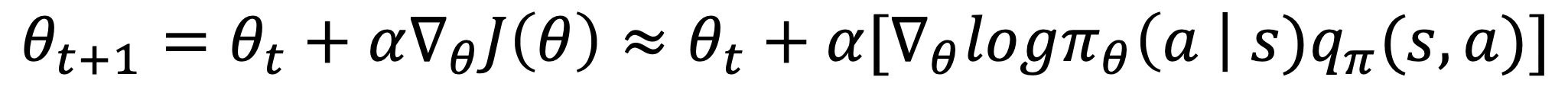
  • 여기서 문제는, 현재 에이전트는 정책만 가지고 있지 큐함수를 가지고 있지 않다는 것이다!
  • 이 문제를 해결하기 위해 큐함수를 근사할 수 있는 반환값으로 대체하는 것이 고전적인 방법이다.
  • 결국 REINFORCE 알고리즘의 업데이트 식은 다음과 같이 완성된다.

사진

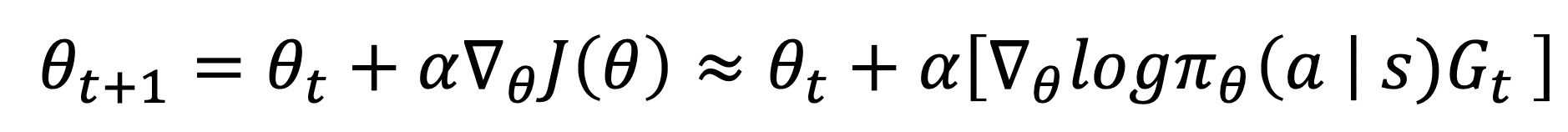
  • 결국 에피소드가 끝날 때까지 기다려서 에피소드 동안 지나온 상태에 대한 반환값을 보내줘야 한다.
  • 에피소드마다 실제로 얻은 보상으로 학습하는 폴리시 그레이디언트이다.
  • 그래서 몬테카를로 폴리시 그레이디언트라고도 부른다.

REINFORCE 코드 설명

이 코드에서는 에이전트가 환경과 상호작용하는 방식은 다음과 같다.

  • 1.상태에 따른 행동 선택
  • 2.선택한 행동으로 한 타임스텝 진행
  • 3.환경으로부터 다음 상태와 보상을 받음
  • 4.다음 상태에 대한 행동을 선택, 에피소드가 끝날 때까지 반복
  • 5.환경으로부터 받은 정보를 토대로 에피소드마다 학습을 진행

이 코드는 에이전트가 정책신경망을 가지고 있기 때문에 그저 정책신경망의 출력을 통해서 행동을 정할 수 있다.

# 정책신경망으로 행동 선택
def get_action(self, state):
    policy = self.model.predict(state)[0]
    return np.random.choice(self.action_size, 1, p=policy)[0]
  • 정책 자체가 확률적이기 때문에 저절로 탐험하게 된다.(탐욕정책 필요x)

에피소드가 끝날 때까지 지속적으로 행동을 선택하고 상태, 행동, 보상을 rewards라는 리스트에 저장해놓는다.

def append_sample(self, state, action, reward):
    self.states.append(state[0])
    self.rewards.append(reward)
    act = np.zeros(self.action_size)
    act[action] = 1
    self.actions.append(act)

그리고 에피소드가 끝나면 에이전트는 그레이디언트를 계산한다. 먼저 rewards로 저장된 리스트로 부터 반환값을 계산한다. 반환값을 계산하는 방법은 다음과 같이 역으로 계산하면 훨씬 간단하다.

사진

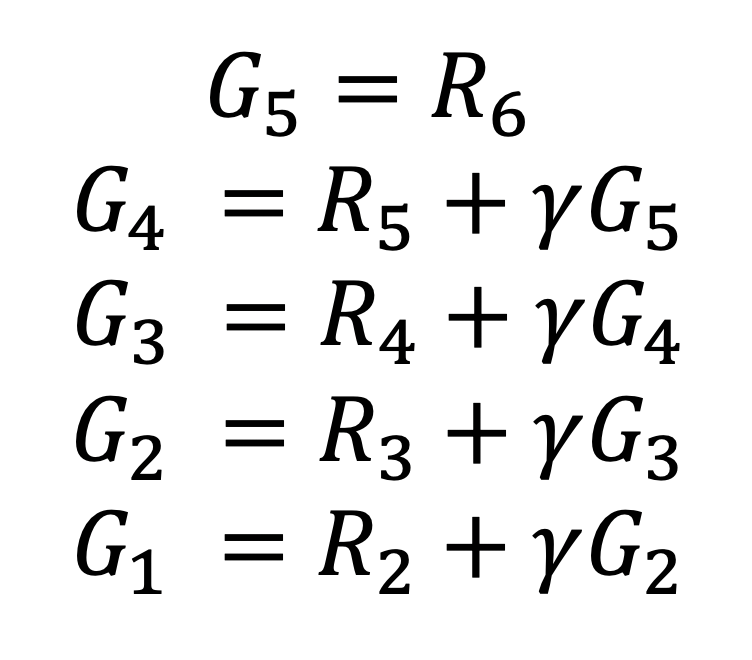
코드로 표현하면 다음과 같다.

for t in reversed(range(0, len(rewards))):
    running_add = running_add * self.discount_factor + rewards[t]
    discounted_rewards[t] = running_add

반환값을 바탕으로 그레이디언트를 계산해서 네트워크를 업데이트하기 위해서는 오류함수를 구해야 한다.

오류함수를 위한 수식은 다음과 같다.

사진

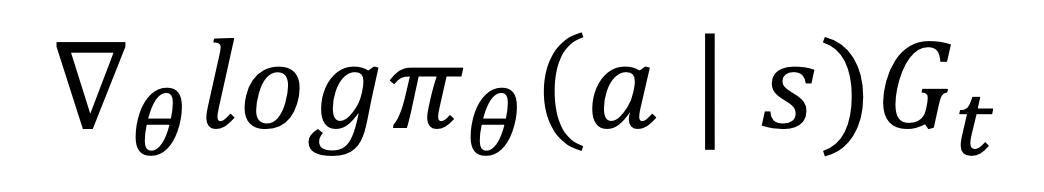
여기서 오류함수를 찾기 위해서 필요한 것이 있는데 바로 크로스 엔트로피이다. 크로스 엔트로피란 y와 p 두 값이 얼마나 가까운지를 보여준다.

사진

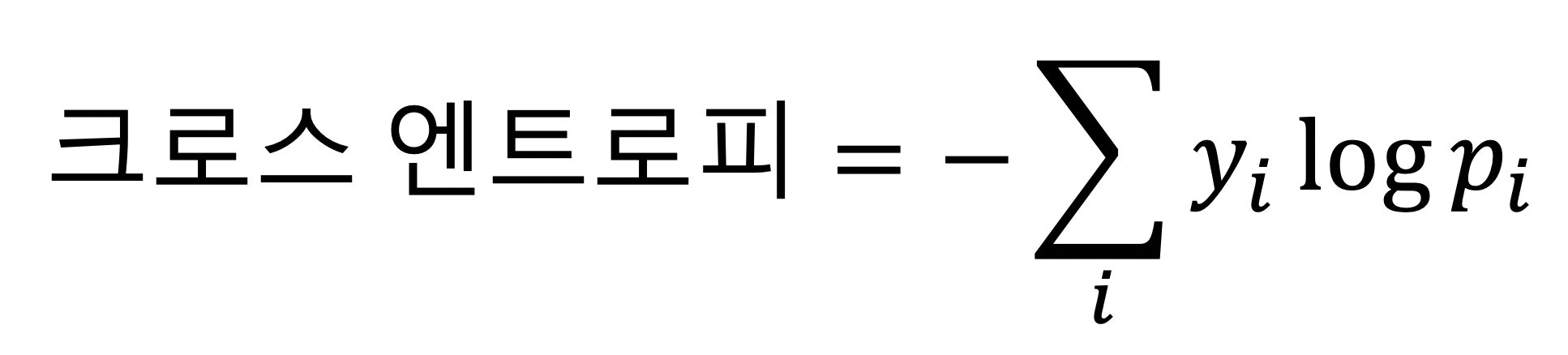
다음 코드에서는 크로스 엔트로피로 오류함수를 찾는 과정을 보여준다.

# 크로스 엔트로피 오류함수 계산
action_prob = K.sum(action * self.model.output, axis=1)
cross_entropy = K.log(action_prob) * discounted_rewards
loss = -K.sum(cross_entropy)

위의 과정을 통해 만들어진 loss가 최종 오류함수가 된다.

결국 에피소드가 진행된 후에는 train_model을 통해서 rewards를 이용해서 정쳑샌경망을 역으로 업데이트한다.

느낀점

  • 이것은 매우 어렵다. 확실히 어렵다…
  • 처음부터 완벽하게 이해하면 좋겠지만 지금 더 하면 재미가 없어질 것 같아서 일단 오늘 공부한 내용에서 손을 떼려고 한다.
  • 확실히 에피소드 하나가 끝나고 나서 학습을 해서 인지 학습 속도는 매우 느리다.
  • 초기에 헤매는 과정이 정말 길다. 하지만 고차원에서는 이러한 정책을 근사하는 방법이 더 용이하다고 한다.
  • 다시 한번 돌아봐야할 것 같다. 오늘은 일단은 고생 많아따….