세그먼트 트리란?

  • 세그먼트 트리는 트리의 각 노드에 어레이 부분부분의 연산 결과를 미리 저장해놓으므로써 탐색 시간을 OlogN)으로 감소시켜준다.
  • 주로 부분합, 부분최소, 최대값을 찾는데 사용된다.

세그먼트 트리 구조

  • 세그먼트 트리의 리프 노드와 나머지 노드는 다음과 같은 의미를 가진다.
  • 리프 노드 : 해당 어레이 값
  • 다른 노드 : 오른쪽 자식과 왼쪽 자식을 연산한 결과 값

구조는 아래와 같은 구조를 가지게 된다.

사진

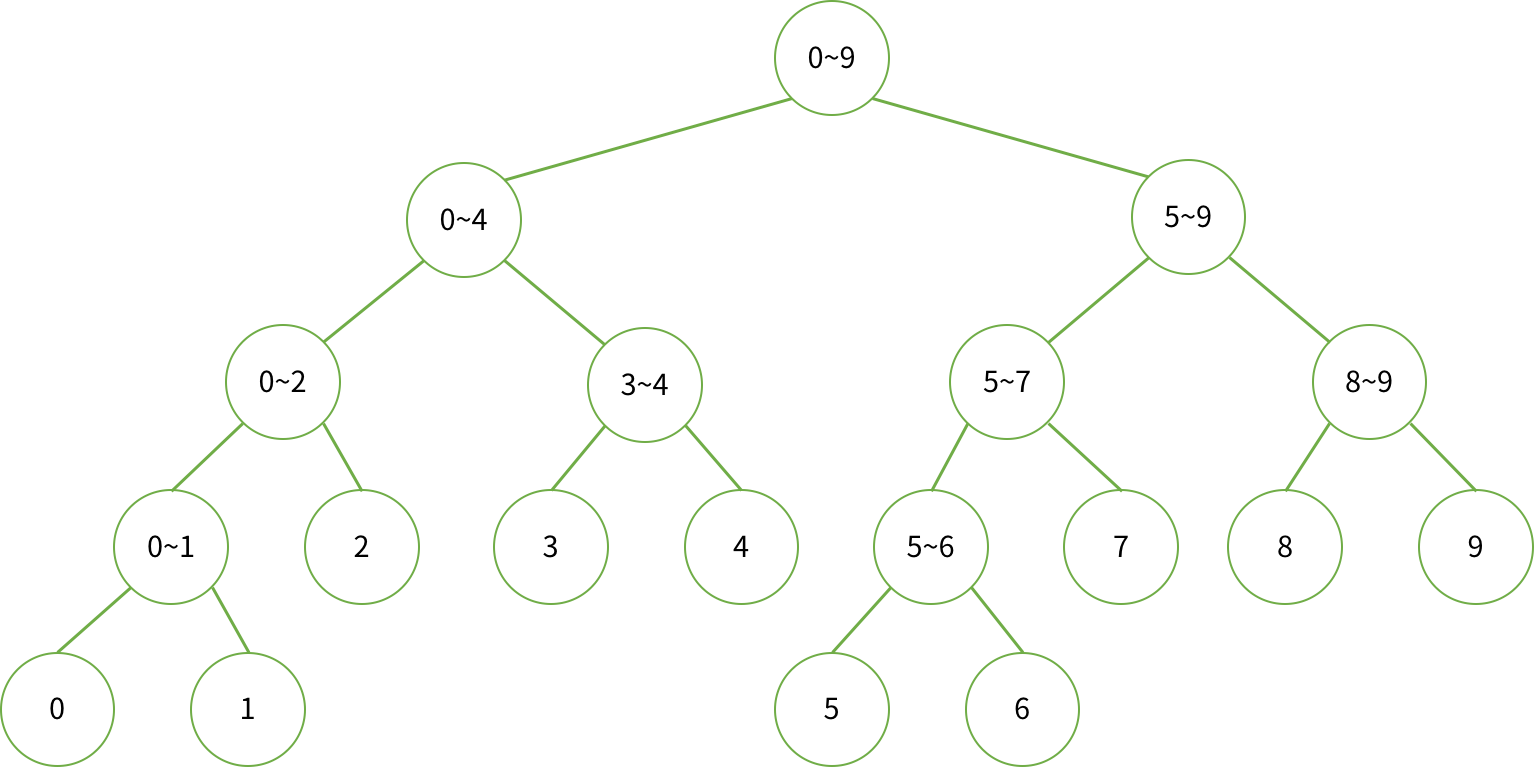
세그먼트 트리 만들기(합 구하기용)

// a: 배열 a
// tree: 세그먼트 트리
// node: 세그먼트 트리 노드 번호
// node가 담당하는 합의 범위가 start ~ end
long long init(vector<long long> &a, vector<long long> &tree, int node, int start, int end) {
    if (start == end) {
        return tree[node] = a[start];
    } else {
        return tree[node] = init(a, tree, node*2, start, (start+end)/2) + init(a, tree, node*2+1, (start+end)/2+1, end);
    }
}

만약 node를 root node로 주고 start, end를 어레이 전체 범위로 잡게 되면 리컬션을 통해 tree가 완성 된다.

세그먼트 트리 탐색(합 구하기용)

만약 어레이 원소가 10개라고 할 때 0-9까지 모든 원소의 합을 찾고 싶다고 하면 아래와 같이 루트 노드만 확인하면 될 것이다.

사진

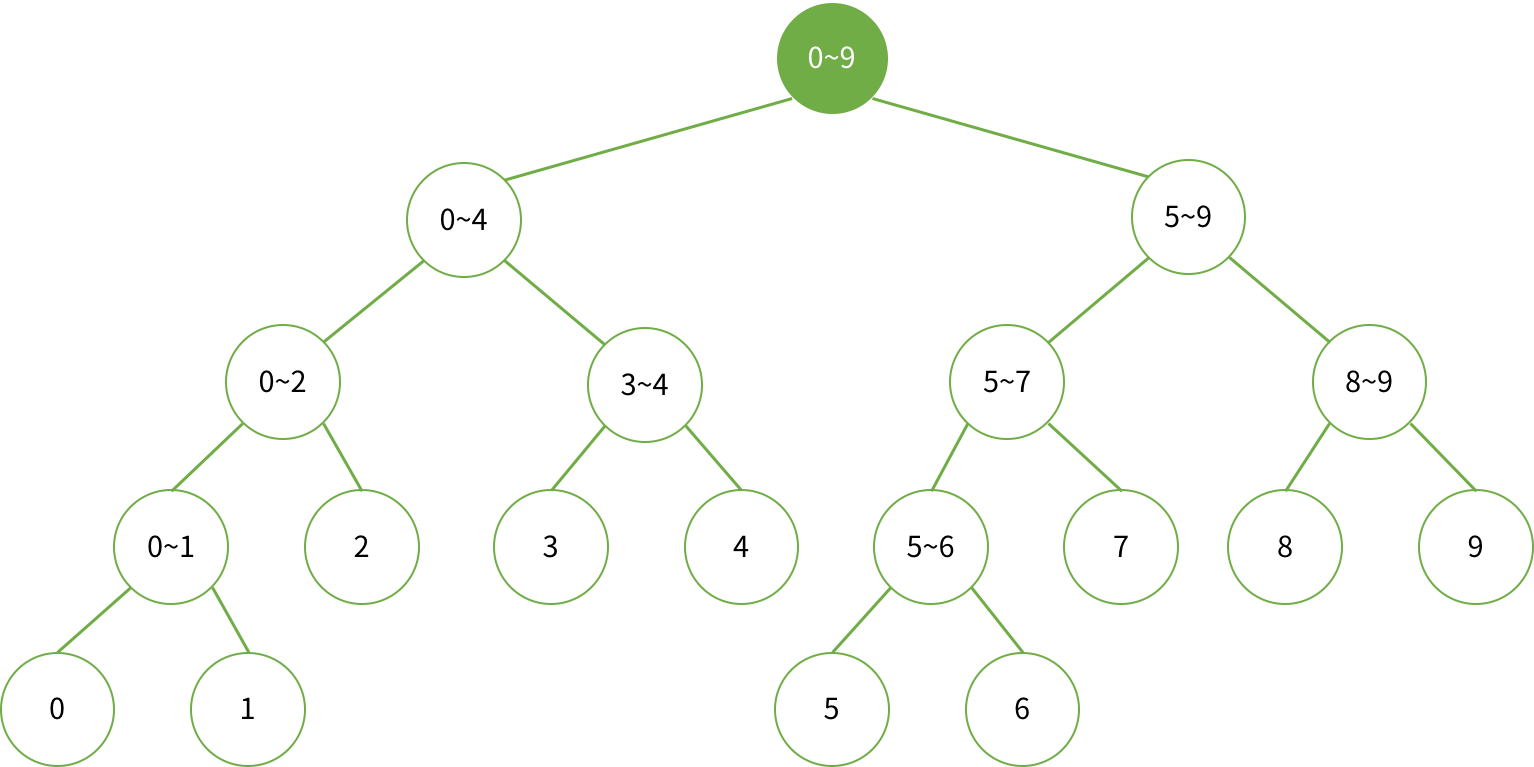
하지만 만약에 2~4까지 범위의 합을 구하고 싶다고 하면 아래와 같이 두개의 원소를 확인하면 될 것이다.

사진

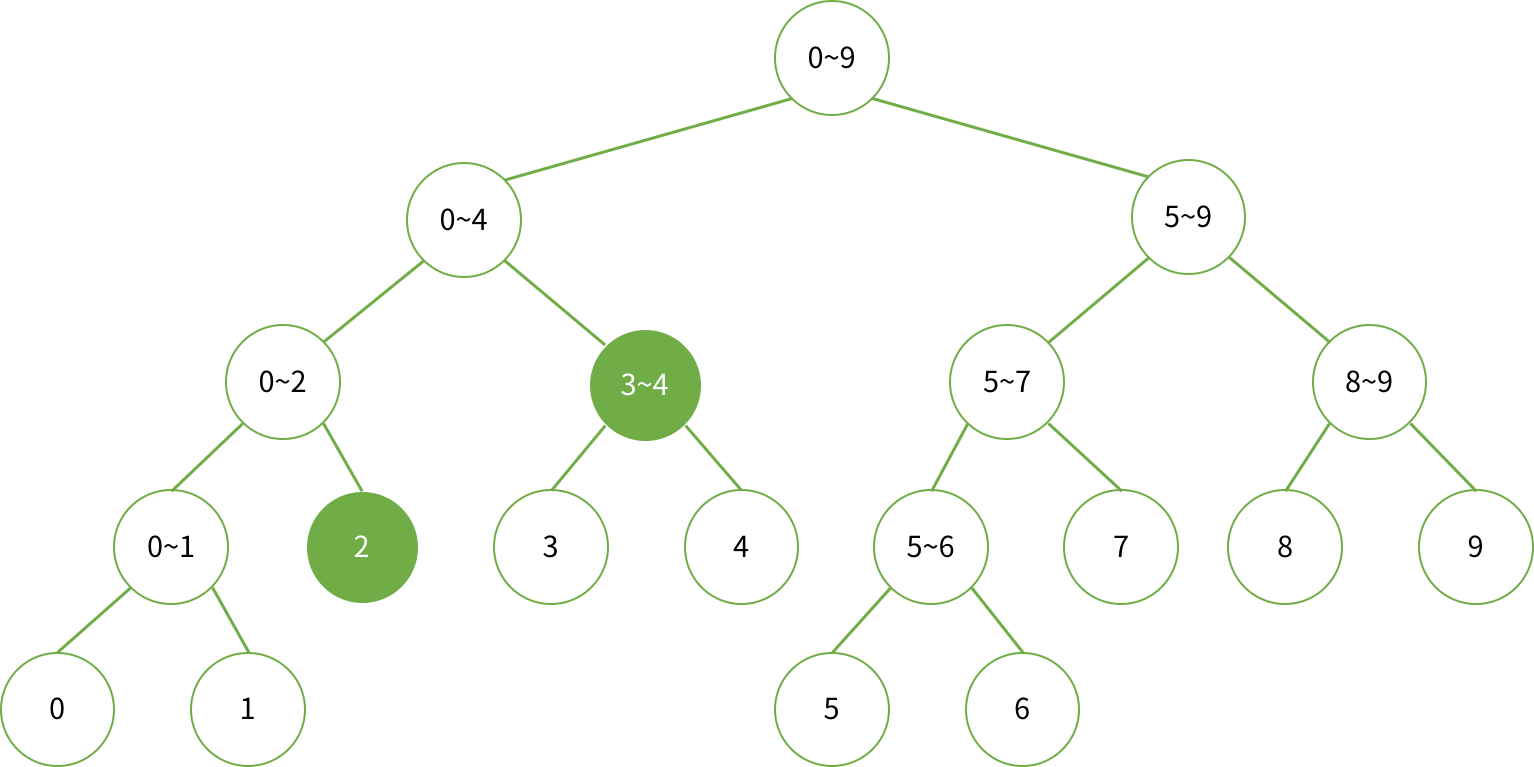
그래서 만약 노드가 담당하는 구간을 [start, end] 라고 하고 합을 구해야하는 구간을 [left, right] 이라 하면 경우는 4가지고 나누어 진다.

  1. [left, right]와 [start, end]가 겹치지 않는 경우
  2. [left, right]가 [start, end]를 완전 커버하는 경우
  3. [start, end]가 [left, right]를 완전히 커버하는 경우
  4. [left, right]와 [start, end]가 부분적으로 겹쳐져 있는 경우
  • 1번 : 무관하기 때문에 합을 구한다고 하면 0을 return하면 된다.
  • 2번 : 더이상 탐색해도 의미가 없기 때문에 현재 노드 값을 return한다.
  • 3번,4번 : 더 쪼개서 다시 탐색을 진행한다.

코드는 아래와 같다.

// node가 담당하는 구간이 start~end이고, 구해야하는 합의 범위는 left~right
long long sum(vector<long long> &tree, int node, int start, int end, int left, int right) {
    if (left > end || right < start) {
        return 0;
    }
    if (left <= start && end <= right) {
        return tree[node];
    }
    return sum(tree, node*2, start, (start+end)/2, left, right) + sum(tree, node*2+1, (start+end)/2+1, end, left, right);
}

6549번 히스토그램에서 가장 큰 직사각형

이 문제에서는 각 segment의 최솟값을 저장해서 최솟값을 더 빨리 찾기 위해 세그먼트 트리가 사용되었다.

코드는 다음과 같다.

#include <cstdio>
#include <vector>
#include <cmath>

using namespace std;
int n, input, answer = 0;

int find_min(vector<int> &a, vector<int> &tree, int node, int start, int end, int left, int right){
    if (left > end || right < start) return -1;
    if (left <= start && end <= right) return tree[node];
    
    int c1 = find_min(a, tree, node*2, start, (start+end)/2, left, right);
    int c2 = find_min(a, tree, node*2+1, (start+end)/2+1, end, left, right);
    if(c1 == -1) return c2;
    if(c2 == -1) return c1;
    return a[c1] < a[c2] ? c1 : c2;
    
}

long long div_and_conq(int left, int right, vector<int> &v, vector<int> &tree){
    int min = find_min(v, tree, 1, 0, v.size()-1, left, right);
    long long box = (long long)v[min]*(long long)(right-left+1);
    if(left <= min - 1){
        long long temp = div_and_conq(left, min -1, v, tree);
        if(box < temp) box = temp;
        
    }
    if(min + 1 <= right) {
        long long temp = div_and_conq(min + 1, right, v, tree);
        if(box < temp) box = temp;
    }
    return box;
}

// a: 배열 a
// tree: 세그먼트 트리
// node: 세그먼트 트리 노드 번호
// node가 담당하는 합의 범위가 start ~ end

void init(vector<int> &a, vector<int> &tree, int node, int start, int end){
    if(start == end) tree[node] = start;
    else{
        init(a, tree, node*2, start, (start+end)/2);
        init(a, tree, node*2 + 1, (start+end)/2 + 1, end);
        tree[node] = a[tree[node*2]] < a[tree[node*2+1]] ? tree[node*2] : tree[node*2+1];
    } 
}

int main(){
    while(1){
        scanf("%d", &n);
        if(n == 0) break;
        answer = 0;
        int h = (int)(ceil(log2(n))+1e-9);
        int tree_size = (1 << (h+1));

        vector<int> v(n);
        vector<int> tree(tree_size);

        for(int i = 0; i < n; i++)scanf("%d", &v[i]);
        init(v, tree, 1, 0, n-1);
        printf("%lld\n", div_and_conq(0, n-1, v, tree));
    }
}

주의할점

  • 벡터를 복사할 거 아니면 parameter로 쓸 때 &를 붙여줘라. 복사하는데 시간이 또 소모된다.