문제

n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

제한사항

  • 섬의 개수 n은 1 이상 100 이하입니다.
  • costs의 길이는 ((n-1) * n) / 2이하입니다.
  • 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
  • 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
  • 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
  • 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예

n costs return
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4

입출력 예 설명

costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.

사진

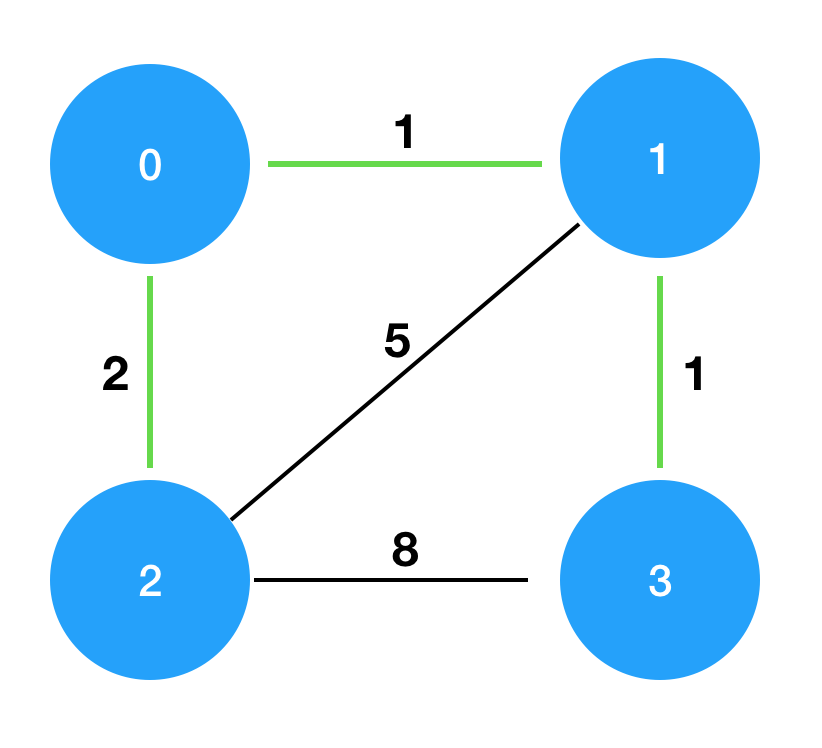
문제 이해

  • 일단 다리를 건너는데 비용을 최소로 하면서 모든 경로까지 갈 수 있는 문제
  • 즉, 이문제는 MINIMUM SPANNING TREE 문제이다!!!!!!!!!
  • 수업시간에 배운거를 써먹어보자아:)

방법은

  • 일단 Minimum spanning tree를 만들 수 있는 Kruskal Algorithm을 사용해보자.
  • sorting해서 작은 weight가 작은 순으로 바꿔놓고 하나씩 끄집어내면서 cycle을 만드는지 확인하고 안만들면 넣어주자.
  • Cycle 확인을 위해서는 Union-Find 알고리즘을 사용해보자.

Kruskal 알고리즘 이용 코드(점수 : 100점)

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

int* parent;

int find(int i){
    if(parent[i] == -1) return i;
    return find(parent[i]);
}

void Union(int x, int y){
    int xset = find(x);
    int yset = find(y);
    if(xset != yset) parent[xset] = yset; 
}

int isCycle(int src, int dest){
    int x = find(src); 
    int y = find(dest);
    if (x == y) return 1; 
    Union(x, y);  
    return 0; 
}

bool compare(vector<int> a, vector<int> b){
    return a[2] < b[2];
}

int solution(int n, vector<vector<int>> costs) {
    int answer = 0;
    int count = 0;

    parent = new int[n]; 

    for(int i = 0 ; i < n; i++) parent[i] = -1;
    sort(costs.begin(), costs.end(), compare);
    for(int i = 0; i < costs.size(); i++){
        if(!isCycle(costs[i][0], costs[i][1])){
            answer += costs[i][2];
            count ++;
            if(count == n - 1) return answer;
        }
    }

    return answer;
}

여기서 오늘 배운 Rank와 Path Compression을 활용한 코드를 또 짜봤다.

Union-Find 강화 코드(점수 : 100점, 속도: 향상)

#include <string>
#include <vector>
#include <algorithm>

using namespace std;
vector<vector<int>> costs;

struct subset {
    int parent;
    int rank;
};

struct subset *subsets;

int find(int i){
    if(subsets[i].parent != i)subsets[i].parent = find(subsets[i].parent);
    return subsets[i].parent;
}

void Union(int x, int y){
    int xroot = find(x);
    int yroot = find(y);
    if(subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot;
    else if(subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot;
    else{
        subsets[yroot].parent = xroot;
        subsets[xroot].rank ++;
    }
}

int isCycle(int t){
    int x = find(costs[t][0]);
    int y = find(costs[t][1]);
    if (x == y) return 1;
    Union(x, y);
    return 0;
}

bool compare(vector<int> a, vector<int> b){
    return a[2] < b[2];
}

int solution(int n, vector<vector<int>> _costs) {

    subsets = (struct subset*) malloc( n * sizeof(struct subset) );
    for (int v = 0; v < n; ++v) {
        subsets[v].parent = v;
        subsets[v].rank = 0;
    }

    costs = _costs;

    int answer = 0;
    int count = 0;

    sort(costs.begin(), costs.end(), compare);

    for(int i = 0; i < costs.size(); i++){
        if(!isCycle(i)){
            answer += costs[i][2];
            count ++;
            if(count == n - 1) return answer;
        }
    }

    return answer;
}

두 알고리즘 시간 차이

</br>

테스트 케이스가 작아서 시간 차이가 크게 안나보이지만 역시 시간이 줄었다 ㅎㅎ 흐뭇하다ㅎㅎㅎㅎ

느낀점

  • 막상 배운 알고리즘 하나 써먹으려고 하니 3시간이 훌쩍 지나가버렸다. 내가 모르는 부분을 타고 타고 들어가서 모르는 부분을 먼저 해결하고 나오다보니 걸린 시간이다.
  • 이시간을 통해서 윤호형이 알려줬던 Union Find에 대해서 배울 수 있었고 Kruskal 알고리즘을 확실히 집고 넘어갈 수 있었으며 Union Find의 강화버전까지 배울 수 있었다.
  • 음.. 시간 대비 효율 이런거 따지기는 뭐하지만 그냥 진짜 공부한 것 같아서 기분이 좋다:)