(백준 알고리즘 문제풀이) 5639번 이진 검색 트리

문제

문제 접근

이 문제는 이진 검색트리와 순회 방법을 이해하고 있다면 충분히 풀 수 있는 문제이다.

이진 검색 트리

이진 검색 트리란 root node의 left subtree에는 항상 root보다 작은 값들이 위치하고 right에는 root보다 큰 값들이 위치한다.

예제 트리도 그런 구성을 가지고 있다.

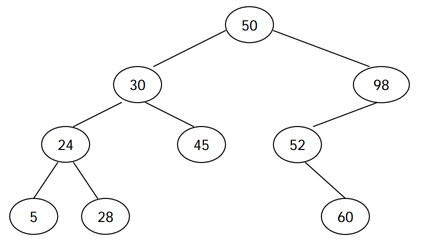
전위순회와 후위순회

전위순회는 root-left-right 순으로 순회하고 후위순회는 left-right-root 순으로 순회한다.

그렇다면 전위 순회 정보에서 특정 범위에서 root의 위치는 알 수 있기 때문에 left와 right는 어디인지를 알아낸다면 굳이 트리를 다시 만들지 않고도 후위 순회 결과를 알 수 있다.

트리의 전위 순회 값이 주어졌을 때, 어디까지가 left subtree의 순회 정보인지를 알 수 없기 때문에 바로 후위 순회 결과를 찾아낼 수는 없다.

하지만 이진 검색 트리는 가능하다!

이진 검색 트리의 순회

이진 검색 트리 전위 순회의 특징은 left에 있는 값들은 무조건 root보다 작다.

반면에 right에 있는 값들은 무조건 root보다 크다. 때문에 root보다 커지는 첫 지점이 right와 left를 구분할 수 있는 지점이라고 볼 수 있다.

이후 재귀를 이용해서 left와 right에 대한 후위 순회를 진행하고 root값을 출력해준다면 자동으로 후위 순회를 출력하게 된다.

코드

#include <iostream>
using namespace std;

int n, x, pre[100000];

void post(int start, int end){
    int root = pre[start], l = start + 1, r = -1;
    //right 시작점 찾기
    for(int i = start; i <= end; i++){
        if(root < pre[i]){
            r = i;
            break;
        }
    }
    //leaf가 아니라면
    if(start != end){
        //left가 있다면
        if(r != l){
            if(r != -1) post(l, r - 1);
            else post(l, end);
        }
        //right가 있다면
        if(r != -1)post(r, end);
    }
    cout << root << '\n';
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);
    while(!(cin >> x).eof()) pre[n++] = x;
    post(0, n - 1);
}

느낀점

처음에는 트리를 만들려고 시도했다가 순간 이진 트리의 특징을 떠올리고 접근 방식을 바꿨다.

이런 식으로 문제를 접근하고 풀 수 있었다는 사실에 감사하다!