문제

2시간반 만에 풀어냈다.. 후우!

문제 링크

문제 요점

  • 여러 개일 수도 있는 최단 경로를 어떻게 빨리 찾아낼지가 제일 중요한 문제이다.

어떻게 접근할 것인가

  • 처음에는 그냥 최단경로를 계속해서 발견할 때마다 prev에 저장해서 다익스트라 알고리즘이 끝나면 최단경로의 prev에 있는 길을 다 차단해주려 했다.
  • 근데 그건 시간 초과를 발생시켰다…
  • 여러번 최단경로를 찾는 것 말고 최단 경로가 한번 발견되면 그 결과를 바탕으로 최단 경로의 길을 다 찾아낼 수는 없을까?

최단경로에 속한 길 찾기

  • 한번의 다익스트라가 끝나면 한점으로부터의 다른 모든 점으로의 최단 경로가 발견된다.
  • 이 특징을 통해 bfs를 이용해서 한번에 찾는 방법을 생각해냈다.
  • 먼저 r이라는 벡터에 길을 방향을 바꿔서 저장한다.
  • 한번 최단 경로를 발견하면 도착점(d)에서 부터 꺼꾸로 BFS를 진행한다.
  • 먼저 도착점을 큐에 넣어준다.
  • 한 점(prev)까지의 최단 경로에 갈 수 있는 길의 길이를 더했는데 front 까지의 최단 경로와 같다면 그 길도 최단 경로의 하나의 길로 큐에 넣어준다.

사진

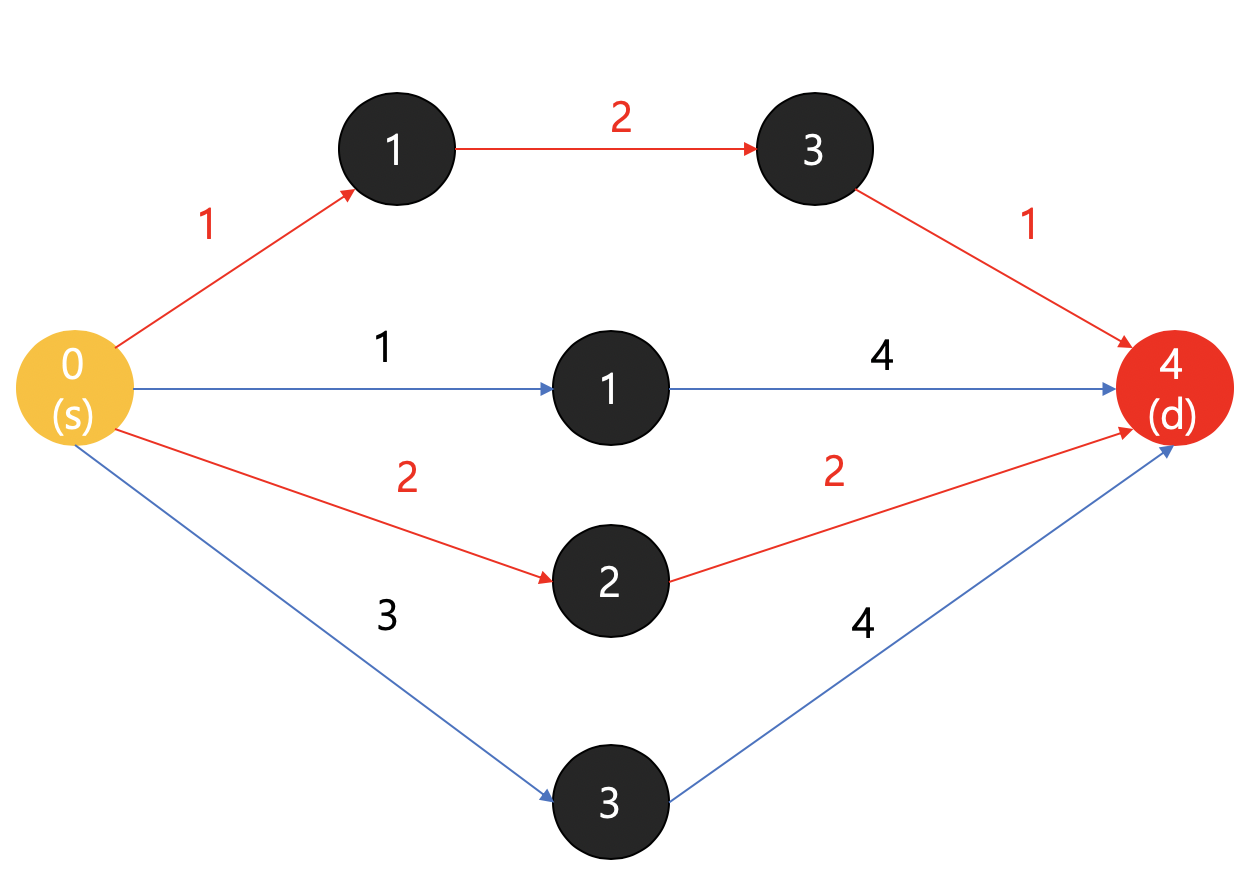
  • 위의 그림에서 빨간색으로 표시한 선들이 모두 최단 경로의 길이다.
  • d에서 부터 시작해서 역으로 dist[prev] + prev_w == dist[front] 인지 확인해준다.

코드

#include <cstdio>
#include <vector>
#include <queue>
#define pii pair<int, int>
#define X first
#define Y second
#define INF 600000

using namespace std;

char buf[1 << 17];

inline char read() {
    static int idx = 1 << 17;
    if (idx == 1 << 17) {
        fread(buf, 1, 1 << 17, stdin);
        idx = 0;
    }
    return buf[idx++];
}
inline int readInt() {
    int sum = 0;
    bool flg = 1;
    char now = read();

    while (now == 10 || now == 32) now = read();
    if (now == '-') flg = 0, now = read();
    while (now >= 48 && now <= 57) {
        sum = sum * 10 + now - 48;
        now = read();
    }

    return flg ? sum : -sum;
}

int n, m, s, d, u, v, p, w, sp;

int findsp(vector< vector<pii> > &e, vector< vector<pii> > &r, vector< vector<int> > &block, int del){
    vector<int> dist(n, INF);
    vector<int> prev;
    priority_queue<pii, vector<pii>, greater<pii> >pq; 

    dist[s] = 0;
    pq.push(pii(0, s));
    while(!pq.empty()){
        int top = pq.top().Y, w = pq.top().X; pq.pop();
        for(int i = 0; i < e[top].size(); i++){
            int next = e[top][i].Y, next_w = e[top][i].X;
            if(!block[top][next] && w + next_w <= dist[next]){
                dist[next] = w + next_w;
                pq.push(pii(dist[next], next));
            }
        }
    }
    if(del){
        queue<int> trace;
        trace.push(d);
        while(!trace.empty()){
            int front = trace.front(); trace.pop();
            for(int i = 0; i < r[front].size(); i++){
                int prev = r[front][i].Y, prev_w = r[front][i].X;
                if(dist[front] - prev_w == dist[prev]){
                    trace.push(prev);
                    block[prev][front] = 1;
                }
            }
        }
    }
    return dist[d];
}

int main(){
    while(1){
        n = readInt(), m = readInt();
        if(!n && !m)break;
        s = readInt(), d = readInt();
        vector<vector<pii> > e(n);
        vector<vector<pii> > r(n);
        vector<vector<int> > block(n, vector<int>(n, 0));
        while(m--){
            u = readInt(), v = readInt(), p = readInt();
            e[u].push_back(pii(p, v));
            r[v].push_back(pii(p, u));
        }
        sp = findsp(e, r, block, 1);
        int t = findsp(e, r, block, 0);

        if(t >= INF) printf("-1\n");
        else printf("%d\n", t);
    }
}

느낀점

  • 문제를 잘 이해했지만 이제는 아이디어 싸움인듯하다.
  • 탐색 알고리즘을 활용하는 방법에 이런 효율적인 알고리즘을 떠올리는 것까지 해야된다니.. 쉽지않다.. 오늘도 참교육ㅠ 그래도 화이팅이다.