(강화학습 입문) 3. 그리드월드와 큐러닝

4장 강화학습 기초 3: 그리드월드와 큐러닝

• 이전에 배웠던 다이내믹 프로그래밍으로 학습시키는 것의 한계인 환경을 알아야 한다는 단점을 극복한 강화학습에 대해 알아보자.
• RL은 에이전트가 환경과 직접 상호작용하며 최적정책을 찾아낸다.

용어 2가지!

• 예측 : 환경과의 상호작용을 통해서 주어진 정책의 가치함수를 학습시키는 것(몬테카를로 예측, 시간차 예측)
• 제어 : 학습한 가치함수를 토대로 정책을 끊임없이 발전시키는 것(살사, 큐러닝)

강화학습과 정책 평가 1: 몬테카를로 예측

사람의 학습 방법과 강화학습의 학습 방법

• 사람의 학습 방법은 환경에 대한 모든 상태에 대한 정확한 지식을 기반으로 학습하지 않는다.
• 대부분 그냥 두면서 결과에 따라서 복기하면서 잘못을 고쳐나간다.

강화학습의 예측과 제어

• 정확하지는 않지만 적당한 추론을 통해서 학습해나가는 것이 실제 세상에서는 더 효율적이다.
• 정책 이터레이션에서 정책 평가는 이 정책을 선택했을 때 얻어지는 참 가치함수를 구하는 과정이지만 강화학습에서 이는 예측이다.
• 예측과 함께 정책을 발전 시키는 것을 제어라고 한다.
• 강화학습은 일단 해보면서 참 가치함수를 예측한다.

몬테카를로 근사의 예시

• 근사란 원래 값을 모르지만 샘플을 통해 원래 값을 추정하는 것이다.
• 다음 그림과 같이 원의 넓이를 구하기 위해 점(샘플)을 찍어보면서 원 안에 있는 점과 그렇지 않은 점을 구분한다.

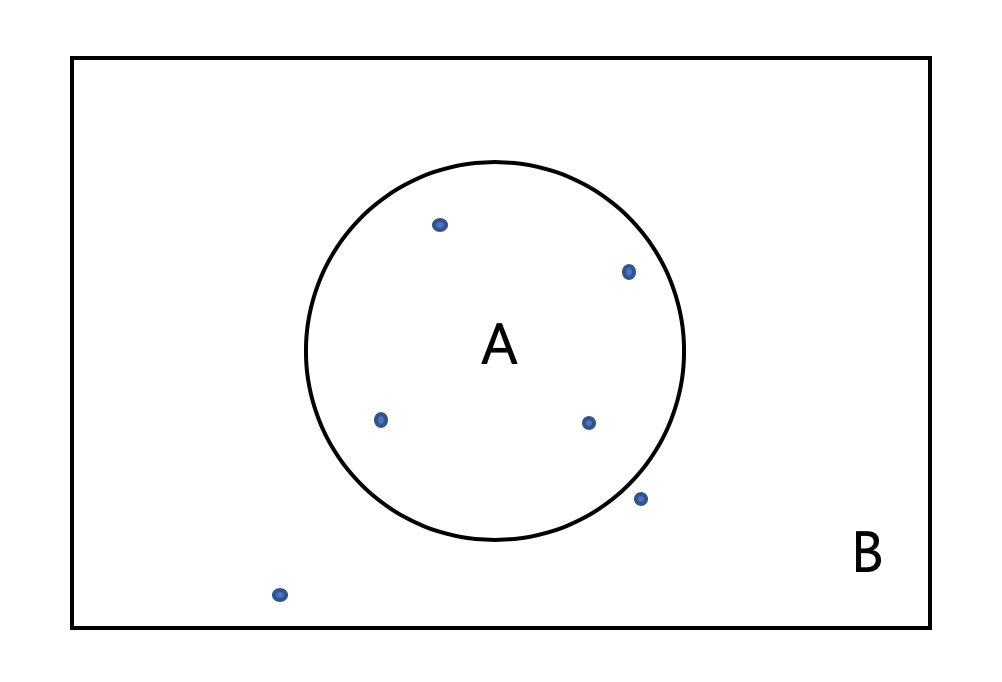
• 점을 무수히 많이 뿌리다보면 A 안에 있는 점의 비율은 실제 B의 넓이와 A의 넓이의 비와 근접해질 것이다.
• 이러한 것을 몬테카를로 근사라 하는데 이는 방정식을 몰라도 원래 값을 추정할 수 있다는 장점을 가지고 있다.

샐플링과 몬테카를로 예측

• 실제 강화학습으로 적용시켜보자.
• 앞에서 점을 찍는 것을 샘플링이라고 한다면 가치함수를 추정할 때는 에이전트가 한번 환경에서 에피소드를 진행하는 것을 샘플링이라고 한다.
• 이 때 샘플링을 통해 얻은 샘플의 평균을 참 가치함수로 추정한다.
• 끝이 있는 에피소드에서 반환값은 다음과 같이 정의한다.

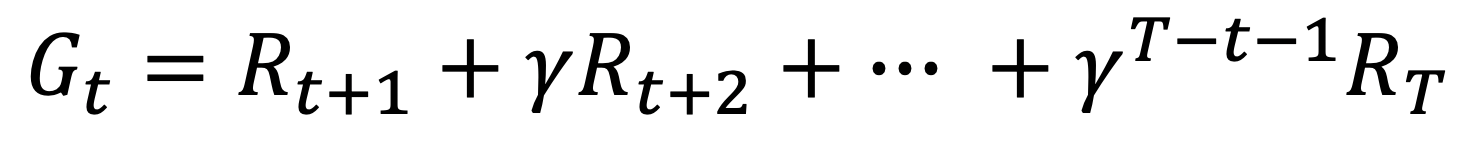
• 각 상태에서 모인 반환값들의 평균을 통해서 참 가치함수의 값을 추정해야하므로 각 상태에 대한 반환값이 많이 모여야한다.
• 벨만 기대 방정식을 계산하려면 환경의 모델을 알아야하지만 여기서는 여러 에피소드를 통해 구한 반환값의 평균을 통해 가치함수를 예측한다.

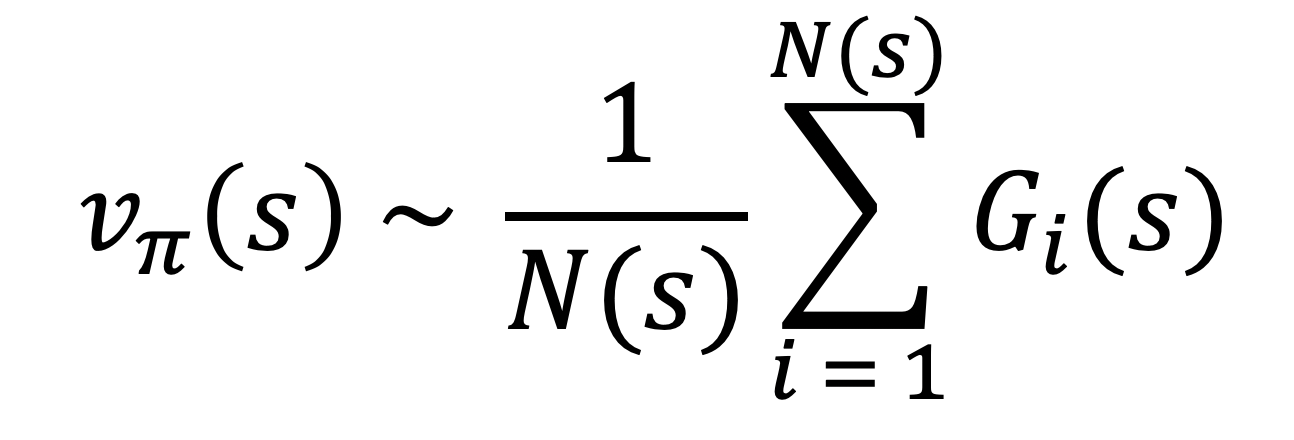
• 이 수식을 다음 과정을 통해서 변경해보았다.
• 새로운 반환값이 추가될 때의 식을 이전 가치함수와의 관계로 나타낸 것이다.
• 새로운 반환값이 추가되면 기존 가치함수에 n/1(Gn - Vn) 값을 더해주어 업데이트 하게 된다.

• 이 때 1/n은 스텝사이즈인데 이것은 오차를 이용해 얼마정도 업데이트할지 정해준다.
• 스텝사이즈는 1/n일 수도 있고 시간에 따라 변하지 않는 일정한 숫자 일수도 있다.
• 이렇게 업데이트 함으로써 가치함수가 이루고자 하는 것은 반환값 자체에 도달하는 것이다.
• 에피소드가 진행될 수록 가치함수가 업데이트 되어가면서 참가치 함수에 수렴해가게 된다.
• 이 몬테카를로 예측의 단점은 에피소드가 끝나야 가치함수가 업데이트 된다는 것이다.

강화학습과 정책 평가 2: 시간차 예측

시간차 예측

• 몬테카를로는 실시간이 아니라는 단점을 가지고 있다. 이를 보완하기 위해 나온 것이 시간차 예측이다.
• 시간차 예측은 타임스텝마다 가치함수를 업데이트한다.
• 반환값에 대한 기댓값으로 가치함수를 정의했던 몬테카를로와 달리
• 다음 식과 같이 리워드와 다음 위치의 가치값으로 현재의 가치함수를 업데이트 한다.

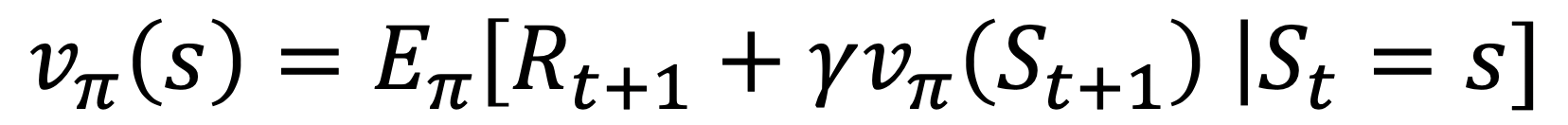
• 에이전트는 매 타임스텝마다 현재 상태에서 행동을 하나 선택하고 환경으로 부터 받을 보상을 알고 다음 상태를 알게 된다.
• 이를 이용해서 가치함수를 업데이트 하게 되면 몬테카를로 예측보다 더 효율적으로 참 가치함수를 찾아낼 수 있다.

강화학습 알고리즘 1: 살사

• 정책 이터레이션과 가치 이터레이션이 어떻게 살사로 발전하는지 알아보자.

살사

• 정책 평가에서 GPI라는 과정을 통해 한번의 평가를 통해 가치함수를 업데이트하고 바로 정책을 발전시키는 것을 반복한다.
• 이러한 과정을 진행하는 것이 몬테카를로 예측과 시간차 예측이다.
• 이 때 시간차 방법에서는 타임스텝마다 현재 상태에 대해서만 가치함수를 업데이트하기 떄문에 GPI처럼 모든 상태에 대해서 발전 시킬 수 없다.
• 이를 해결한 방법이 바로 가치 이터레이션의 탐욕정책을 사용하는 것이다.
• GPI의 탐욕정책은 다음과 같다.

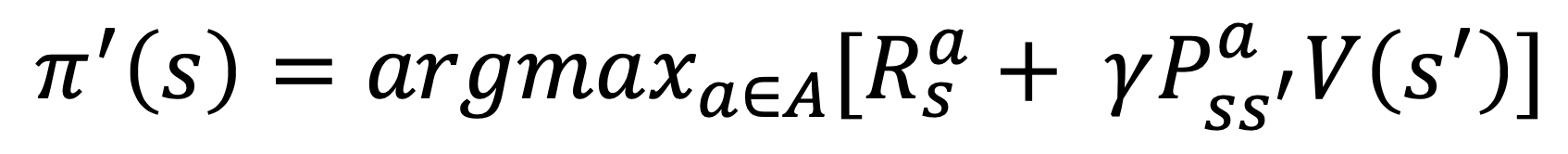
• 이때는 환경모델인 P를 알아야 한다.
• 하지만 만약 현재 상태의 큐함수를 보고 판단한다면 환경 모델을 몰라도 된다.
• 따라서 수식은 다음과 같이 된다.

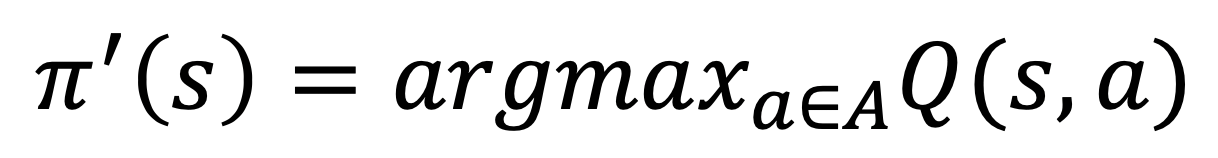
• 큐함수에 따라 행동을 결정하려면 에이전트는 가치함수가 아닌 큐함수의 정보를 알아야 한다.
• 이 때 시간차 제어의 식은 다음과 같다.

• 큐함수를 업데이트 하기 위해 필요한 정보는 S, A, R, S’, A’ 이므로 이를 살사라고 부른다.
• 여기서 강화학습의 중요한 탐험의 문제가 나온다.
• 많은 경험을 한 에이전트의 경우 탐욕 정책이 가장 좋은 선택이겠지만 초기 에이전트의 탐욕 정책은 잘못된 학습으로 가게 할 가능성이 크다.
• 때문에 다음과 같이 일정한 확률로 탐욕적이지 않게 하는 E-탐욕정책이 필요하다.

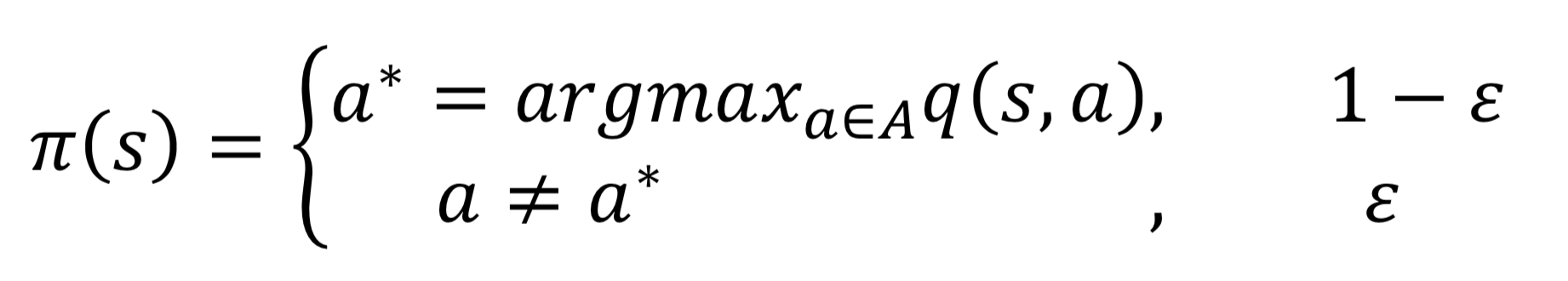
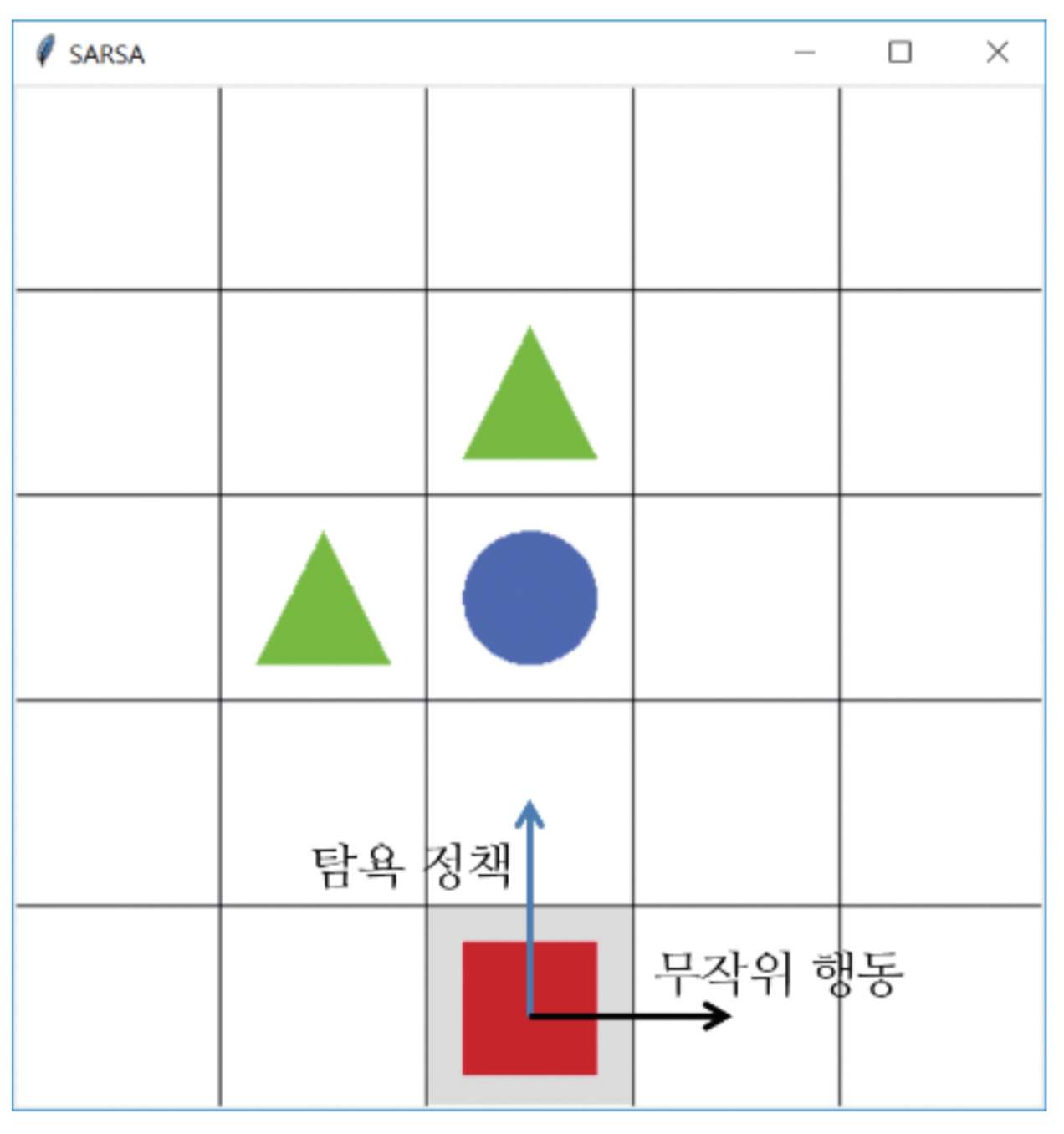
• 따라서 일정한 확률로 무작위한 행동을 하게 한다.
• 여기서 문제는 최적의 큐함수를 찾았다고 하더라도 일정한 확률로 계속 탐험한다는 한계가 있다.

강화학습 알고리즘 2: 큐러닝

살사의 한계

• 충분한 탐험을 위해 사용한 E-탐욕 정책이 다음과 같은 상태에서 문제를 야기할 수 있다.

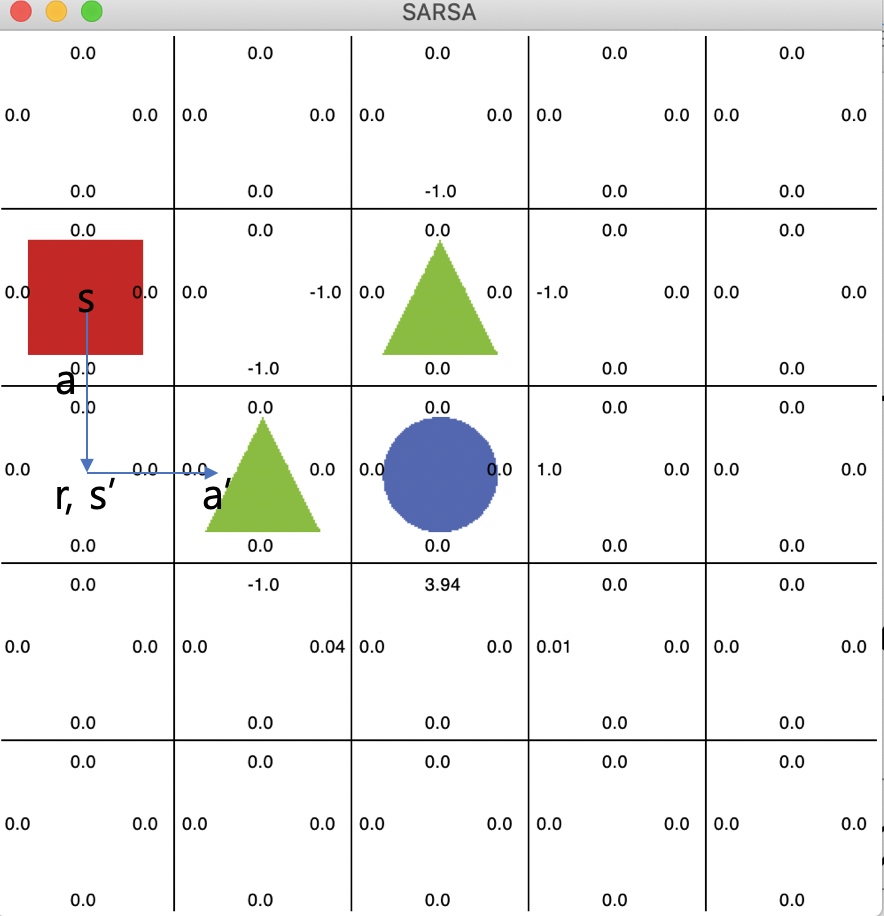
• 초기 에이전트가 만약 s에서 a라는 행동을 하고 다음 행동인 a’은 탐험을 통해서 가게 되었다고 생각해보자.
• 그럼 자연스럽게 초기 에이전트는 Q(s,a) 값을 낮출 것이고 이에 따라 s에서 아래로 이동하는 행동이 안좋다고 판단할 것이다.
• 결국 에이전트가 특정 state에 갇혀버리는 현상이 발생한다.
• 이렇게 자신이 행동한 대로 학습하는 것을 On-Policy 시간차 제어라고 한다.
• 이러한 딜레마를 해결하기 위해 사용하는 것이 바로 오프폴리시 시간차 제어, 큐러닝이다.

큐러닝 이론

• 큐러닝은 행동하는 정책과 학습하는 정책을 따로 분리해둔다.
• 살사에서는 다음 상태 s’에서 또다시 탐욕정책을 따라 다음 행동을 선택한 후에 그것을 학습에 샘플로 사용한다.
• 반면에 큐러닝에서는 다음 상태 s’를 알게 되면 그 중에 가장 큰 큐함수를 업데이트에 사용한다.

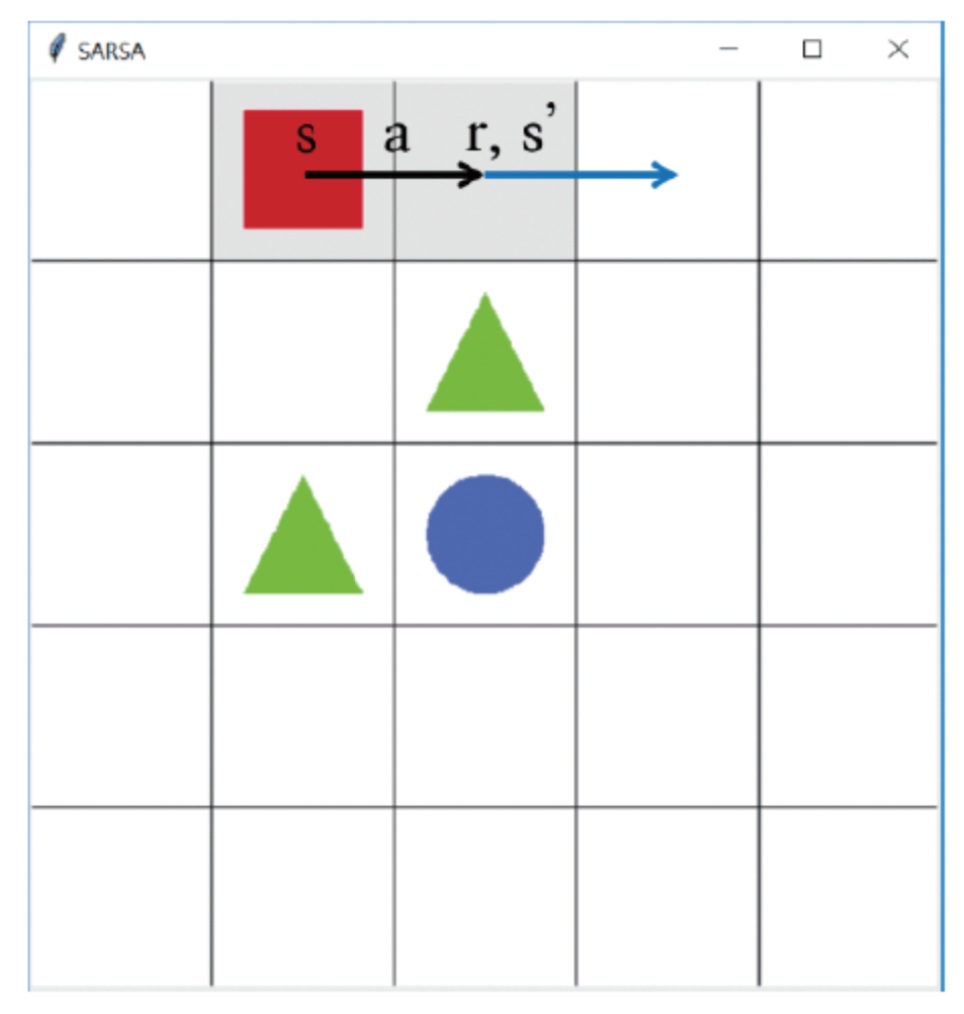
• 다음 상태에서 어떤 행동을 했는지보다 그냥 큐함수의 베스트를 고르게 된다.
• 따라서 큐함수를 업데이트하기 위한 샘플은 [s,a,r,s’]이 된다.
• 이는 결국 s’에서 한 실제 행동이 초록색 세모로 가는 안좋은 행동일지라도 현재 상태 s를 업데이트하는 것에는 반영되지 않기 때문에 구석에 갇히는 문제가 발생하지 않는다.

정리

• 몬테카를로 예측 : 샘플링(에피소드 끝의 반환값)을 통한 평균으로 대체하는 방법, 에피소드가 끝나야 값을 안다는 한계
• 시간차 예측 : 매 타임스텝마다 가치함수 업데이트
• 살사 : 환경 모델을 알아야하는 가치함수가 아닌 큐함수로 제어, E-탐욕정책으로 인해 고립될 수 있다는 한계
• 큐러닝 : 살사의 한계를 개선, 행동하는 정책과 학습하는 정책을 분리(s, a, r, s’를 샘플로 받음)

느낀점

• 몬테카를로도 알겠고 이해는 조금씩 해가는 것 같다.
• 막상 이제 점점 더 알아갈수록 내가 실제로 구현할 수 있을지 불안하다.
• 본격적으로 이게 공프기 주제가 되었으니 이제는 진짜 빠꾸없이 열심히 해봐야겠다.
• 간잽이는 할만큼 했다!