(강화학습 입문) 1. 강화학습 소개 및 MDP와 벨만 방정식 정리

동기

육목 블로그 게시글을 따라가면서 육목도 알파고 제로처럼 만들 수 있겠다고 생각했다. 미리 짜놓은 코드를 이해하면서 Game.py 정도를 수정하면서 알고리즘을 만들어보려 했지만 제일 핵심이 되는 모델을 이해하지 못하고 이를 접목시키는 것은 배울 수 있는 것이 얼마 없다는 생각이 들었다. 결국 진혁이형한테 이 얘기를 했더니 책을 하나 딱 가져다 줬다.

파이썬과 케라스로 배우는 강화학습!

부제가 내 손으로 직접 구현하는 게임 인공지능이다…ㅋㅋㅋㅋ 너무 조아~~~

괜히 갇진혁형이 아니었다. 뭔지 모르고 따라가는 것보다 조금 체계적으로 이해하면서 공부해보려 이 책을 읽어보기로 마음을 먹었다. 하나하나 차근차근 읽으면서 정리해보려고 한다.

1장 강화학습 소개

여기 파트는 자기전에 쭉 읽어봤는데 내가 보기에 좋았더 내용만 미리 정리해본다.

강화학습 개념

• 강화학습이란 마치 사람처럼 환경과 상호작용하면서 스스로 학습하는 방식을 말한다.
• 강화학습은 결정을 순차적으로 내려야 하는 문제에 적용된다.
• 강화학습은 머신러닝의 한 분야이지만 데이터로 부터가 아닌 행동에 대한 보상으로 학습하게 된다.
• 게임에 대한 규칙을 몰라도 학습할 수 있다는 것은 장점일 수도 있지만 초반의 느린 학습의 원인이 되기도 한다.

약간 의문인 내용

“사람은 하나를 학습하면 다른 곳에도 그 학습이 영향을 미칩니다. 하지만 현재 강화 학습 에이전트는 각 학습을 다 별개로 취급해서 항상 바닥부터 학습해야 합니다.

그러면 초기에 내가 어느정도 좋은 길을 가르쳐주는 게 불가능하다는 건지 의문이 생겼다.

2장 강화학습 기초 1: MDP와 벨만 방정식

MDP

MDP란 Markov Decision Process의 약자로 순차적으로 행동을 결정해야 하는 문제를 수학적으로 표현한 것이다.

MDP는 다음과 같은 요소들로 구성되어 있다.

• 상태(S), 행동(A), 보상함수(R), 상태변환 확률(P), 감가율(D)

상태(S)

• 정확히 말하면 에이전트가 관찰 가능한 상태의 집합이다.
• 예를 들어, 5X5 그리드 월드에서는 상태집합을 다음과 같이 표현할 수 있다.
• S= { (1,1),(2,1),(1,2),⋯, (5,5) }
• 상태는 시간에 따라 변하므로 각 시간의 상태를 소문자 s로 표현

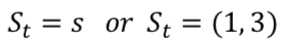
• 이 때 대문자로 나타내는 것은 확률변수(어떤 집합 안에서 뽑을 때 마다 달라질 수 있는 것들)이다.

행동(A)

• 에이전트가 취할 수 있는 행동의 집합이다.
• A = {상, 하, 좌, 우}
• 각 시간에 취한 행동을 소문자 a로 표현한다.

보상함수(R)

• 에이전트가 한 행동에 대한 환경이 제공하는 피드백이다.
• 보통 +, -로 표시한다.
• 시간이 t이고 상태 s에서 a를 선택했을 때 받는 보상은 다음과 같다.

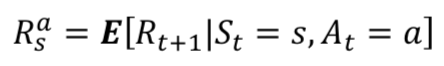
• 보상은 현재 시간이 받는 것이 아니라 t+1이 전달받는다.
• 이 때 보상은 E(기댓값)으로 전달된다. 그 이유는 환경에 따라서 같은 상태와 행동에도 보상이 다를 수 있기 때문이다.
• 기댓값이란 어떤 정확한 값이 아니라 나오게 될 숫자에 대한 예상이다.

상태 변환 확률(P)

• s에서 a라는 행동을 통해 s’로 이동을 한다고 했을 때 s에서 s’으로 상태가 바뀔 확률을 말한다.
• 확률적인 요인에 의해 s’에 도달하지 못할 수도 있다.

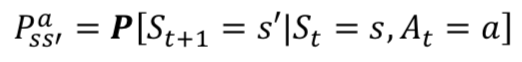
• 이 값은 에이전트가 가지고 있는 것이 아니라 환경이 가지고 있는 것이다.
• 이 확률을 알면 디피, 모르면 RL, 섞으면 Dyna-Q란다.

감가율(할인율)(D)

• 에이전트가 현재에 판단을 내리므로 현재 받을 수 있는 보상과 미래에 받을 수 있는 보상에 구분을 두어야 한다.
• 미래에 받을 보상은 현재 상황 받을 수 없으면서 할인율을 곱해 감소시킨다.
• 할인율은 0과 1 사이 수이다.
• 파란색 원에 도달할 때 주어지는 보상은 각 위치에 대해 아래와 같이 할인율이 곱해진다.

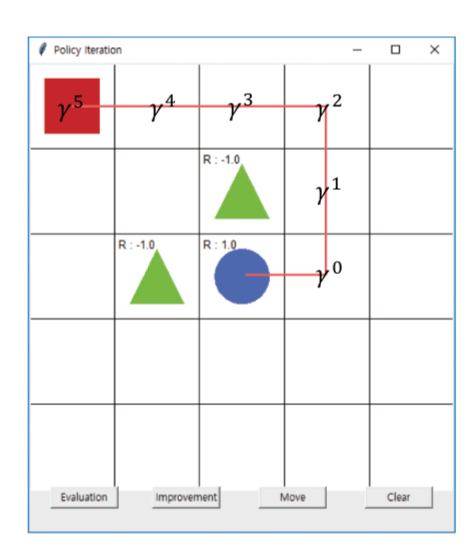
MDP 정리

그리드 월드 문제에 있어서 MDP는 다음과 같이 볼 수 있다.

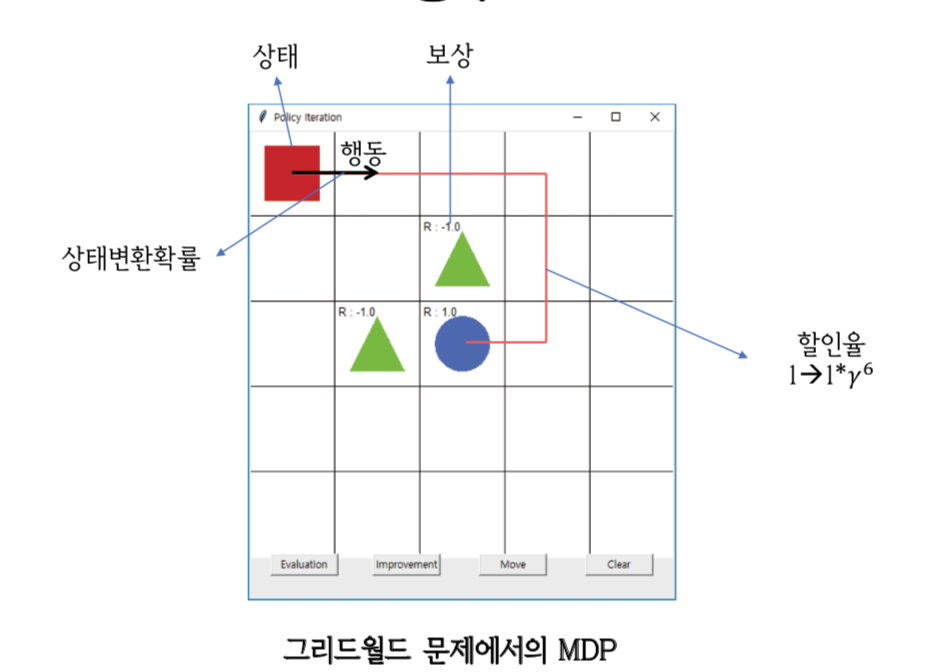
할인율의 5승을 곱해줘야하지 않나 싶다.

정책(Policy)

• 에이전트가 각 상태에서 어떻게 행동할지에 대한 정보를 가지고 있다.
• 최적 정책은 하나의 행동만을 선택하지만 에이전트가 학습 중일 때는 확률적으로 여러개를 선택할 수 있어야 한다.

• 따라서 정책은 P[At = a

  St = a]로 나타낼 수 있다.

• 그리드월드의 정책값은 다음과 같다.

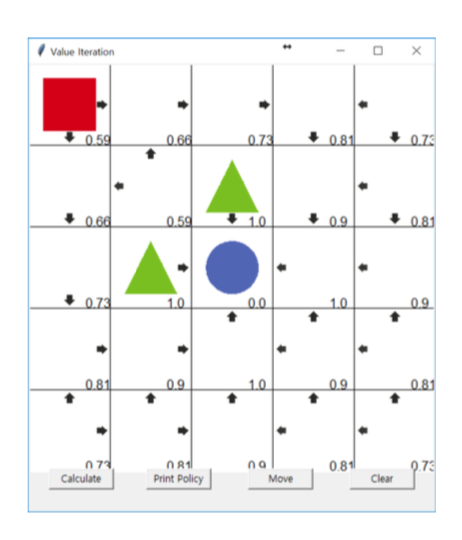
MDP 에이전트의 행동 선택

자, 그렇다면 여태까지 MDP에 대해서 알아봤는데 에이전트는 매번 어떻게 행동을 선택할까?

단기적 보상

• 에이전트와 환경의 상호작용을 통해서 얻게 된다.
• 1.에이전트가 상태를 관찰하고
• 2.가치함수에 따라 행동을 선택하고
• 3.환경으로부터 보상을 받는다.

여기서 문제가 있다. 에이전트는 매 타임스텝 마다 가장 보상을 많이 받으려고 한다. 그런데 그렇게 단기적인 보상만 고려한다면 최적의 정책에 도달할 수 있을까?

• Sparse Reward(바둑, 육목과 같이 승패가 늦게 알려짐)
• Delayed Reward(선택한 행동에 대한 보상이 나중에 알려짐)

그럼 장기적인 보상은 어떻게 알아낼 수 있을까?

장기적 보상1. 단순합

• 앞으로 받을 모든 합을 더한다.

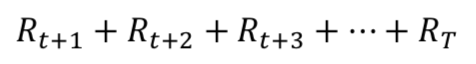
• 한계1: 지금 받은 보상이나 미래에 받는 보상이나 똑같이 취급한다.
• 한계2: 단순한 보상의 합으로는 판단을 내리기 쉽지 않다.

장기적 보상2. 반환값

• 감가율을 고려하여 보상 값을 얻는다.
• 에피소드가 다 끝난 후에 그동안 받았던 보상을 정산한다.
• 그에 대한 수식은 다음과 같다.

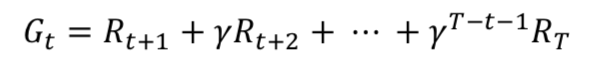
• 한계 : 에피소드가 다 끝난다음에야 그 반환값을 알 수 있다.

꼭 에피소드가 끝날 때까지 기다려야 하나? 이를 개선한게 가치 함수!

장기적 보상3. 가치함수

• 가치함수에서는 에이전트가 다 직접 경험해보지 않고 기댓값에 의해서 보상을 예측한다.
• 대신 이는 정책에 영향을 많이 받는다.
• 상태 s로만 정해지는 값으로 가능한 반환값들의 평균을 구해서 진행한다.
• 수식은 다음과 같다.
• 이 수식이 강화학습에서 진짜 중요한 벨만 기대 방정식이다.

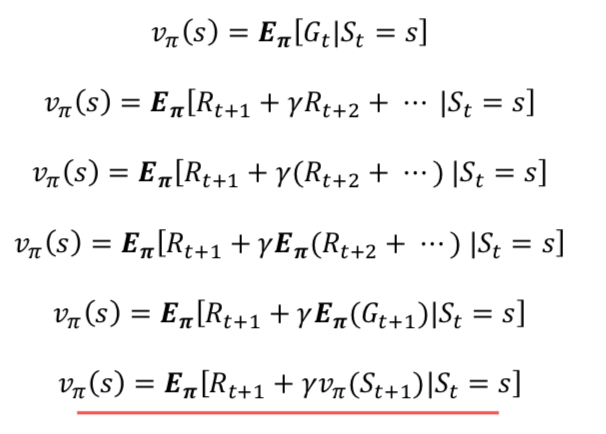
큐함수(행동 가치함수)

• 앞서 본 수식은 상태가 입력으로 앞으로 받을 보상의 합을 출력해주는 함수이다.
• 큐함수란 굳이 다음 상태의 가치함수를 따져보지 않고 현재 상태와 행동만으로 가치를 판단할 수 있게 해주는 함수이다.
• 강화학습에서는 큐함수를 기존 가치함수보다 더 많이 사용한다.
• 기존 가치함수 식과 다른 점은 조건에 행동이 하나 더 들어간다는 점이다.

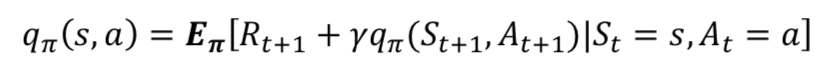
벨만 방정식

벨만 기대 방정식

왜 벨만 기대방정식이 강화학습에서 중요한 위치를 차지하고 있는가?

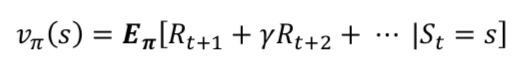
• 위의 수식과 같이 반환값으로 기댓값을 알아낸다고 하면 모든 보상을 계산해봐야 한다.(현실적으로 말이 안된다.)
• 그래서 아래 수식과 같이 식 자체로 풀리지는 않지만 계속 계산을 하는 방식을 이용해서 푼다.

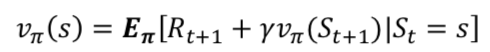
벨만 최적 방정식

• 벨만 기대 방정식을 이용해 현재의 가치함수를 계속 업데이트하다 양변이 같아 지는 수렴 상태가 된다.
• 이 가치함수를 참 가치함수라고 하는데 이 친구는 최적 가치함수와는 다르다.
• 최적 가치 함수란 가장 높은 보상을 얻게 하는 가치 함수를 말한다.
• 최적 큐함수도 마찬가지이다.

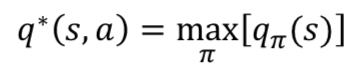
• 이때 큐를 최적으로 찾아주는 함수인 argmax를 통해서 최적 정책을 찾아낼 수 있다.

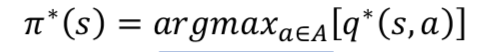
• 가치함수와 큐함수에 대한 벨만 최적 방정식은 다음과 같다.

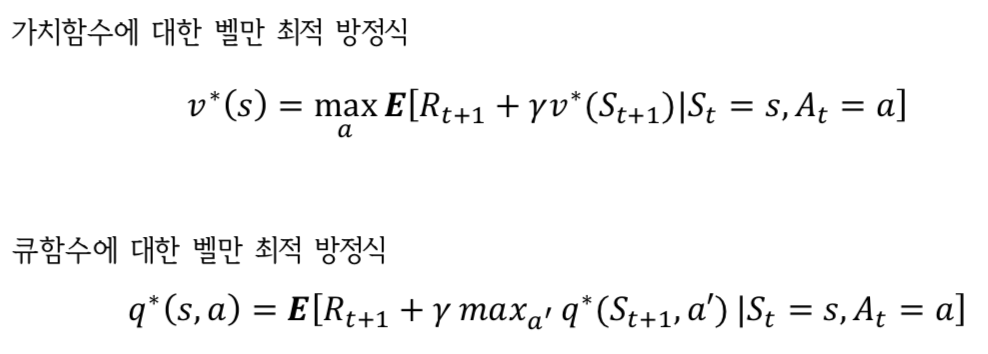
느낀점

• MDP에 대한 이해는 어느정도 한것 같은데 최적 벨만 기대 방정식을 구하는 과정은 정확히 이해하지 못한 것 같다.
• 필요하다면 나중에 다시 한번 도전해보자!
• 일단 재미있게 오늘 공부를 마무리한 것에 감사하다!